In the last few years, SAMPEX researchers and others have become increasingly interested in transient belts created by injection of particles during geomagnetically disturbed conditions. The example that springs to mind first, for most of us, is the intense belt of ultrarelativistic electrons injected into the "slot" region between the usual inner and outer radiation belts on 24 March 1991; however, most such injections of protons and electrons are of much lesser intensity, and they may be difficult to see above the steady background of the Earth's radiation belts (especially the inner belt). We have found, however, that the low-altitude orbit of SAMPEX allows us to see these transient belts more readily when we look in regions of the magnetosphere where the Earth's atmosphere has "scrubbed away" the particles that elsewhere contribute to the long-lived radiation belts, and where only relatively recently-injected particles are present. These regions are referred to as the "drift loss cone"; this webpage provides a qualitative, graphical explanation of this concept.
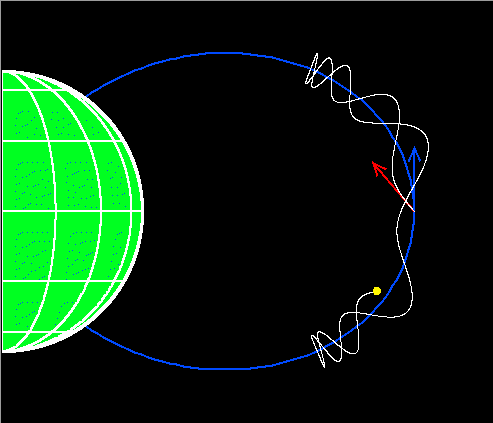
We begin with some basic characteristics of the motion of charged particles in a dipolar magnetic field, which is a pretty good approximation to the Earth's field close to the planet (there are small, higher-order contributions to the field--quadrupole, octupole, etc.--which we ignore in this discussion, and we also consider only the near-Earth region where distortions of the field by magnetopause currents can be neglected). A charged particle will gyrate around the magnetic field line, clockwise or counterclockwise depending on the sign of its electrical charge, and it will also bounce up and down the field line, "mirroring" and reversing direction at symmetrical points above and below the magnetic equator, as shown in the figure below (projecting the particle trajectory into a meridional plane).

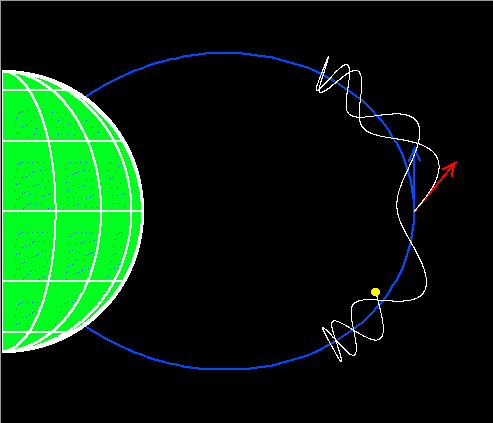
Exactly how far the particle gets from the magnetic equator before "mirroring" is determined by its pitch angle at the equator; this is the angle at the equator between the velocity of the particle (red arrow) and the magnetic field (blue arrow), or 40 degrees in this plot. A particle with a pitch angle nearer to 90 degrees at the equator will mirror at a lower latitude (and a higher altitude) along the field line, as seen in the following diagram of the motion of a particle with an equatorial pitch angle of 60 degrees, which mirrors closer to the equator (and farther away from the planet) than the particle in the figure above.
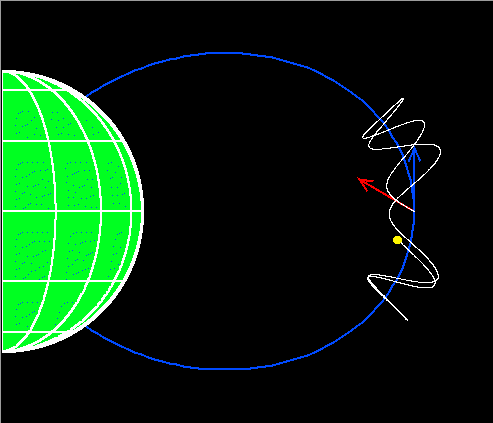
(A particle with an equatorial pitch angle of 90 degrees, moving perpendicular to the magnetic field there, will "mirror" at the equator and thus will remain in the magnetic equatorial plane.) To first order, the "gyrophase" of a particle (its position in its gyration circle about the magnetic field) at the equator does not affect the latitude (or altitude) at which the particle mirrors; this is a function only of the equatorial pitch angle. This is seen in the following diagram of the motion of a particle with an equatorial pitch angle of 40 degrees as in the figure at top, but with a gyrophase 180 degrees different from that of the particle in the first figure: the particle mirrors at about the same latitude (and altitude) as in the first figure.
It can be seen that if a particle's pitch angle is close enough to 0 or 180 degrees (that is, nearly enough aligned with the magnetic field), then its mirror point will fall below the surface of the planet (actually, below the thickening atmosphere at about 100 km altitude) and it will be lost before completing a full cycle of bounce motion. If we ignore gyrophase, the set of velocity vectors at the equator of particles that will be lost in this way forms a filled double-ended cone from zero degrees to some critical pitch angle alpha, and from 180 degrees to (180 degrees minus alpha). This set is termed the "bounce loss cone," or simply "loss cone," and may be represented by the red cone of velocity vectors relative to the blue magnetic-field vector in the left-hand figure below.
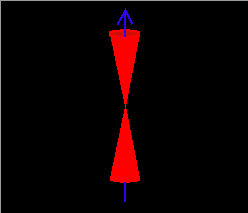
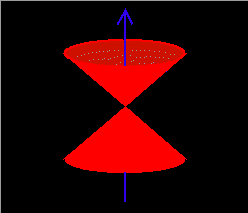
It can also be seen that (1) as the point of observation moves along the field line away from the equator, a given particle's local pitch angle (angle between local velocity vector and local magnetic field direction) will steepen from its equatorial value toward 90 degrees as its mirror point is approached; and (2) at any given location away from the equator, there will be particles that are not observed since their mirror points are at lower latitudes. Thus the bounce loss cone at different points along the field line, defined in terms of local (rather than equatorial) velocity vectors relative to the local (rather than equatorial) magnetic field, will widen as latitude increases (and altitude decreases), as in the right-hand figure above, until it reaches 90 degrees opening angle and all particles are in the loss cone (0 to 90 degrees and 90 to 180 degrees in the two directional cones) when the point of observation reaches the top of the atmosphere.
The magnetic field of a dipole possesses cylindrical symmetry about the dipole moment vector, which is up-and-down in the figures above; thus one can find corresponding magnetic field lines of the same size and (at corresponding points) field strength in any meridional plane, and this set of field lines defines a toroidal "L shell," where L is the radius (in units of Earth radii) of the circle defined by the intersection of these field lines with the magnetic equator (about 3 in the above figures). As particles gyrate around the magnetic field and bounce up and down the field lines, they also drift around the planet, as sketched in the following figure (eastward for negatively-charged particles, westward for positive), with drift periods of seconds to days for particles in the energy range observed by the SAMPEX instruments.
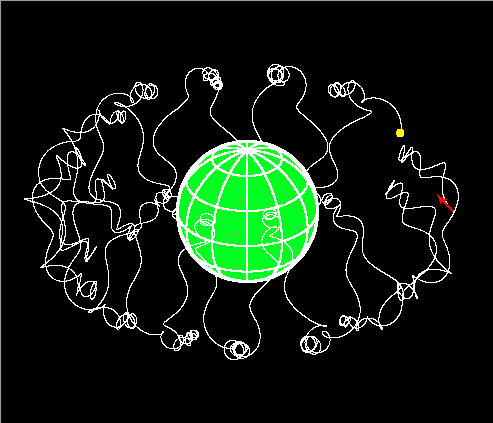
The mirror points always occur at the same field strength on each bounce, i.e., at the same latitude away from the magnetic equator. (Actually, this statement, like the one above that mirror-point location is independent of gyrophase, is only true to the extent that the particle's radius of gyration, or "cyclotron radius," is small enough relative to the field-line size that many gyrations occur on each bounce and many bounces on each drift around the planet, not the measly dozen or so depicted (for clarity) in the figures above!)
The figures above were sketched for a dipolar magnetic field centered on the Earth's center. However, a better approximation is to have the center of the dipole offset from Earth's center, and its vector moment tilted relative to the Earth's axis; the particle motions will then still be (approximately) symmetric with respect to the offset, tilted dipole field, but not relative to the Earth's axis and equator, as in the figure below (with offset exaggerated relative to Earth's actual configuration, for clarity).
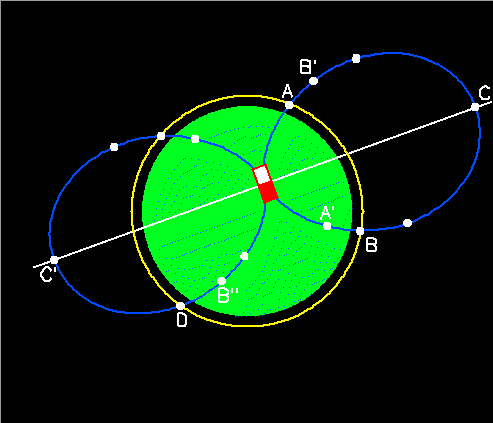
Charged particles' mirror points will still be symmetric about the magnetic equator (white line), but will no longer be symmetric either between hemispheres or in longitude relative to the planet. Thus a polar-orbiting, low-altitude satellite like SAMPEX can make observations of different subsets of the particle population as its orbit (yellow circle) crosses a given L shell (blue) in different quadrants. Consider the particles observed at point A in the figure; they are safely above the atmosphere (at least, as long as SAMPEX is!), but on their next bounce they will attempt to mirror at or below point A' and will be lost into the atmosphere. Thus the bounce loss cone extends to 90 degrees at point A (the particles with pitch angles slightly less than 90 degrees will not hit the atmosphere before mirroring once in the northern hemisphere, but once they reverse direction they will be lost in the southern hemisphere before completing a full cycle of bounce motion, and thus they are considered to be in the bounce loss cone), and despite being safely above the atmosphere, the point of observation is said to be "in the bounce loss cone" since all particles observed there are.
Now consider the particles observed at point B; particles with pitch angles near 90 degrees there will not hit the atmosphere below point B in the southern hemisphere, and they will mirror at high altitude near point B' in the northern hemisphere, and therefore the bounce loss cone is less than 90 degrees in size (point B is not "in the bounce loss cone"). However, as these particles drift around the planet, eventually they will attempt to mirror near point B'' and will be lost. These particles, then, will be in the equatorial bounce loss cone at point C' (since they will encounter the atmosphere before completing a full cycle of bounce motion) but not at point C; at point C we say that these particles compose a "drift loss cone," in that they will encounter the atmosphere before completing a full cycle of drift motion. The relationship between the bounce (red) and drift (yellow) loss cones about the magnetic field (blue) at point C is shown in the left-hand figure below.
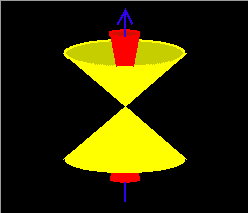
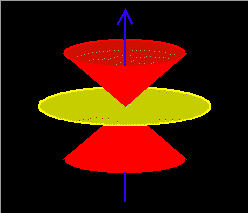
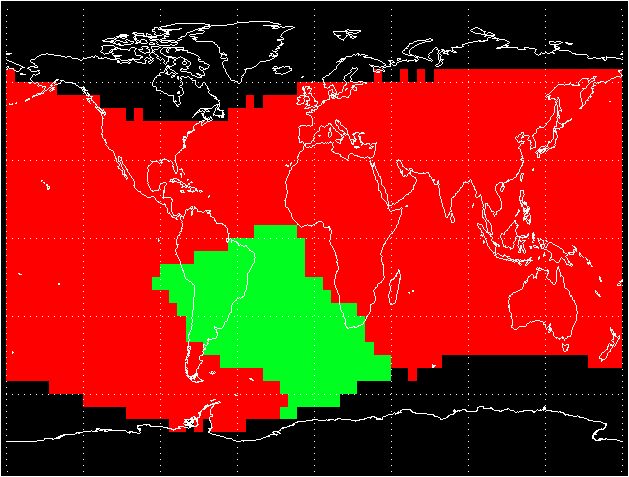
As the point of observation moves along the field line from point C toward point B, the respective loss cones will widen as described above, until all particles observed are in the drift loss cone (and some are also in the bounce loss cone) as in the right-hand figure above, so the point of observation is said to be "in the drift loss cone" since all observed particles are. The plot below, based on calculations of Michael Redding and Michael McNab at The Aerospace Corporation, shows geographic locations in a 600-km orbit (this was the average altitude of SAMPEX at launch) where a satellite observes only particles in the drift and/or bounce loss cones (colored red) and where it observes some particles that are stably trapped outside the loss cones (colored green). Only locations where L shells less than 4 are encountered have been colored in, because at high latitudes (and high L values) the field lines are so far above the Earth at the equator that the distortions due to magnetopause currents can no longer be ignored, as we assumed above. The green region corresponds to the South Atlantic Anomaly, which is the portion of the Earth's actual field represented by point D in the mirror-point diagram above: particles that the satellite sees outside the bounce loss cone here will mirror at high altitudes everywhere else on their drift trajectories, and thus can remain trapped for a long time.
The usefulness of this concept is that particles in the drift loss cone do not have long lifetimes--ions will last less than one drift period, and the majority of electrons (those that don't backscatter when encountering the atmosphere) will be lost in less than one drift period. Thus the steady background of the inner zone in particular, which consists mostly of particles with a lifetime of months to years, will be scrubbed away in the drift loss cone on a timescale short compared with the mean lifetimes of particles in the inner zone, and therefore anything we see in the drift loss cone must be a recent addition. This is not to say that the particles must come from a population that was injected less than one drift period ago; however, the population must scatter in pitch angle so that the drift loss cone is repopulated on a timescale comparable to the drift period, and therefore the main population will be eroded on something like this timescale, so it can't be too old. Since the SAMPEX orbit is such that the spacecraft spends a lot of time in the drift loss cone, it is in a unique position to "lie in wait" for these rare injection events and to observe even the smaller ones that would be unnoticeable outside the drift loss cone, and therefore unobservable by a higher-altitude satellite.
(P.S. Actually, another sort of drift loss cone is defined at higher altitudes, based on the field distortions due to magnetopause currents that we ignored here: particles may encounter open field lines or the magnetopause itself before completing a complete drift around the planet, and be lost thus. The region where these effects occur is, however, well outside the inner magnetosphere where transient belts are injected and where we use the drift loss cone as defined above to observe them.)
 Back
to top of Data Pages
Back
to top of Data Pagesnew 9 October 2000